wave equation

A useful solution to the wave equation for an ideal string is:

 y(x,t) = Asin(2π/λ(x+/-vt))

This is a solution to the one-dimensional wave equation (via direct substitution):


∂ ² / ∂x² = (ρ/T)(∂²y/∂t²)

giving us:

1 =  (ρ/T)v²

giving the wave velocity of a stretched string:
v = √(T/ρ)
where T = tension in the string

and the mass her unit length:
ρ = m/L

Useful links

Useful resources:


http://www.physics.buffalo.edu/phy207/lc/lc15.pdf

http://hyperphysics.phy-astr.gsu.edu/hbase/waves/wavsol.html#c1



Identities to know:

     cos(x+λ) = cos(x)     and   λ = 2π
cos(x + λ/2) = -cos(x)   and   λ/2 = π
cos(x + λ/4) = -sin(x)   and   λ/4 = π/2


LOCATIONS OF THE WAVE ANGLE MAXIMA AND MINIMA
ΔL = dsin(θ)

MAXIMA:
ΔL = nλ

MINIMA:
ΔL = (n + 1/2)λ

The principle of superposition

From Mastering Physics:


The principle of superposition states:

If two functions each separately satisfy the wave equation, then the sum (or difference) also satisfies the wave equation. This principle follows from the fact that every term in the wave equation is linear in the amplitude of the wave.

Consider the sum of two waves y1(x,t)+y2(x,t), where y1(x,t) is the wave described in Part A and y2(x,t) is the wave described in Part B. These waves have been chosen so that their sum can be written as follows:

y_s(x,t) = y_e(x)y_t(t)


This form is significant because:

 y_e(x) called the envelope, depends only on position

 y_t(t) depends only on time


Traditionally, the time function is taken to be a trigonometric function with unit amplitude; that is, the overall amplitude of the wave is written as part of ye(x).



COMBINING TWO WAVES TO CREATE A STANDING WAVE:

y1(x,t)=Asin(kx−ωt).

y2(x,t)    = Asin(kx+ωt)
y1(x,t)= 
  y1(x,t)=

Consider the sum of two waves y1(x,t)+y2(x,t)

Their sum can be written as follows:
ys(x,t)=ye(x)yt(t).

ye(x), yt(t) =

2Asin(kx),cos(ωt)

New topic ... Optics / waves and light!

MECHANICAL WAVES

General equations:

Amplitude in Simple Harminoc Motion (SHM): A = $\sqrt{\mathrm{Xi^2\; +\; (V^2/\omega \; ^2)}}$
 where ω = $\sqrt{\mathrm{k/m}}$

Phase angle (SHM): Φ = arctan(-Vi/ω xi)
 where ω = $\sqrt{\mathrm{k/m}}$$$$$

Phase: (kx-ωt) is a constant wavelength: λ = 2π/ω UNIT: meter


frequency: f = 2π/ω UNIT: cycles/second

NOTE THAT ω also equals: ω = νk 

wavespeed or speed of propagation: ν = $\sqrt{\mathrm{T/\mu }}$ UNIT: meters/second

ν = fλ

k = 2π/λ 

General Transverse Equation: y(x,t) = Acos2π([x/λ]-[t/T]) 

 Tension: μv = (mass of rod/length of rod)(frequency•wavelength)


POWER

Power: P = (force)(velocity) 

 P = 4πr^2(Intensity)

Converting power to energy? multiply by Joules! 1 W = 3.6x10^3 Joules

Ch 34: electromagnetism

To end the "Electricity and Magnetism" series of blogs; one *must* see this astounding video on the beauty of science in our everyday world:

http://youtu.be/sEw-v4yQxek

Amperes FULL Law; (A law that describes nature perfectly): 

Maxwell discovered that there was a missing link in Amperes original law! 

This link is responsible for describing the change in electrical field causes by a change in magnetic field. 

Maxwell determined that electromagnetic  waves have a speed - which is how light travels. Maxwell determined that the speed of light (experimentally known at the time) is the SAME speed as electromagnetic waves. Thus, Maxwell is responsible for determining that light itself is an electromagnetic disturbance.

Online slides from Texas U that are helpful for reviewing:

http://www.ph.utexas.edu/~phy317n/PHY317L/Lectures/ch29-notes.pdf

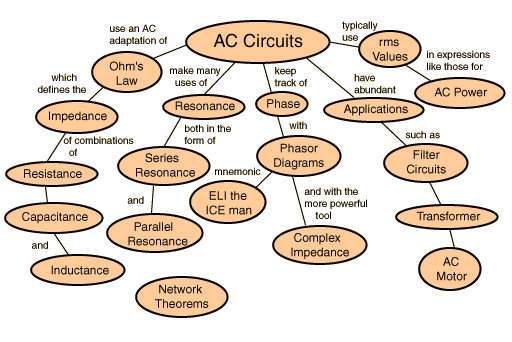
Chapter 33: AC Circuits

Alternating Current Circuits

source for image: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/accircon.html#c1

Equations to remember:

when an AC Circuit switch is closed, we have a charging circuit, and:

I = deltaV/R

voltage across the inductor equals 0, and delta V = 0

• instantaneous voltage and current are 90 degrees out of phase, where V lags behind I within the capacitor
• instantaneous voltage and current are 90 degrees out of phase, where V leads I within the Inductor
• voltage is IN PHASE With the current, within the resistor

DeltaVoltageAVG = 1/2VAVG

DeltaVrms = DeltaVmax / sqrt(2)

Inductive Reactance: XL = ωL

Capacitive Reactance: XC = 1/ωC

TOTAL reactance of an RLC circuit:

XL - XC = Rtan(theta)

theta = angle I is leading V

impedance (Z):  Impedance is ...?

Z = SQRT(R^2 + X^2)

Z = V / I

NOTE: V and I are complex sinusoidal functions for voltage and current


**when you have an AC (Oscillating voltage) Circuit that only contains an INDUCTOR,

I = Vrms / ωL

**when you have an AC (Oscillating voltage) Circuit that only contains an CAPACITOR

I = V / XC
I = VωC

The PHASE ANGLE..

in a series RLC circuit the phase angle is given by: tan(theta) = (XL - XC/R)

at resonance, Inductive Reactance equals the Capacitive Reactance:

XL = XC

Phase angles are frequency dependent~!

Power in an electric circuit

RATE OF power delivered (or work done by power) = (frequency) ( voltage)

when F and V are vectors..

P = FVcos(theta)

Quality Factor (Q)

Q tells you how underdamped an oscillator is In physics and engineering the quality factor or Q factor is a dimensionless parameter that describes how under-damped an oscillator or resonator is,^[1] or equivalently, characterizes a resonator's bandwidth relative to its center frequency.^[2] Higher Q indicates a lower rate of energy loss relative to the stored energy of the resonator; the oscillations die out more slowly

source: Wikipedia

Capacitance for an AC-circuit?

UNIT for C = FARADS (F)

C = 1/[4(pi)^2*frequency^2*(L)]

Chapter 32: Inductance

This chapter is about the Inductance (L)

An Inductor is a coil of wire - a miniature solenoid - used in circuits to oppose sudden changes in current. 

Inductors don't like change. They will do anything to oppose change! 

Inductors like to build up a magnetic field within themselves (to store energy) -  this inhibits the flow of current through the circuit.

Once a magnetic field is done being "built" inside the inductor - current flows freely around the circuit! 

Remember: Inductors are pretty useless unless current is changing (increasing or decreasing). 

The capacity of an inductor is a factor of its geometry (area, radius, space between coils) and the number of coils (n).

Summary of main concepts:

Source: http://hyperphysics.phy-astr.gsu.edu/hbase/electric/indtra.html

under construction