Chapter 31: Faraday's "Law"

Previously, we have only studied time dependent situations (Maxwell's 4 equations and the Lorenz Force) 
^Electric and Magnetic fields always obey these rules for time INdependent situations^
E fields analyzed in this situation are conservative forces: that is why the surface integral of E dot dl equals zero! *image required here

This chapter introduces TIME DEPENDENT situations!

If we have a situation where either the scalar quantity for Charge Distribution (UNIT: Coulombs/meters^3) or the vector quantity for Current Density (Unit: Amps/meters^2) changes, then, we have a time dependent situation! Now, we have a non-conservative electrical field to deal with!

Faraday's "Law" of induction: 

Basically, the "law" states that when you move a charged closed loop/coil around/across a magnetic field, (where the movement of the object is in the same plane as the loop) an INDUCED CURRENT will create its own magnetic field!

THEREFORE: we have our Initial Current, I, and our Induced Current, i

AND: we have our Initial Magnetic Field, B, and our Induced Magnetic Field, b

• The "law" is written as:  

• And we define emf as: 

Where F is the Lorentz force. When the movement of an object is NOT in the same plane as the loop, we use the Lorentz force!

pictorial summary of facts:

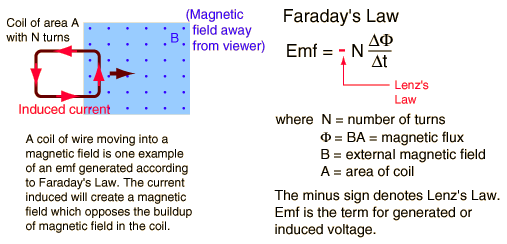
Image is from the following awesome physics website:

http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/faracon.html#c1

recall:

for a uniform field and area, flux = BA when B and A are perpendicular

...SO why did we put "quotes" around the word law?

Because Faradays "law" only works when we are analyzing the velocity of a time dependent object that is moving in the same field as the current carrying loop. This 'situation' commonly occurs - but - does NOT ALWAYS occur!

What about other situations? 

WE KNOW THAT changing the magnetic field changes the electric field

WE KNOW THAT changing magnetic flux (B field or the area) induces an emf

WE KNOW THAT the existence of an emf + wire = Current (I)

SO Faraday's equation is not always able to "SEE" a current. 

recall, 

When the movement of an object is NOT in the same plane as the loop, we use the Lorentz force!

OR, we can use the............

Maxwell-Faraday Law: A Fundamental Law of Nature!
...A summary of the methods voltage can be generated by changing the magnetic field or flux...

Maxwell derived this by combining Faraday's "law" and the definition of emf to hold true for all situations!

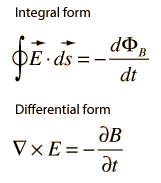
the Maxwell-Faraday equation does not equal zero!

the Maxwell-Faraday equation does not need a physical LOOP of wire, you can analyse the situation with an imaginary loop/path

DEFINITION of Faraday's "Law"

A changing flux induces an emf, or potential difference, in a loop. Whenever we have a potential difference we have an electric field. If the potential difference is the induced emf, we get:
e = ò E ds

The integral should be carried out over a closed loop so we can bring in the changing flux in that loop:
e = -dF_B/dt

This gives, integrating around a closed loop, the general form of Faraday's Law:
ò E ds = -dF_B/dt

Electric fields produced by changing magnetic fields have some interesting properties:

• the electric field lines are continuous loops
• the electric field is non-conservative

TO conclude, we have to visit the topic of the conservation of energy - since we started this blog discussion on equations that describe time dependent situations as NON conservative..

LENZ'S LAW is a statement about the conservation of energy in time dependent situations 

• The current produced from a time dependent situation always works against the action/movement/flow that created the change in flux. 

in other words: the induced current cannot be in the same direction as the original current.

"Eddy Currents" are a result of this...to be continued...

Chapter 30: Magnetic Field Sources

DEFINITION:

Diamagnetic - substances with weak magnetic moments opposite to the applied magnetic field
Paramagnetic - substances with weak magnetic moments in the same directions as the applied magnetic field
Ferromagnetic - substances with magnetic moments between atoms that align to create strong magnetization, which remains after the external magnetic field is removed.

Magnetic flux through a closed surface is:

Biot - Savart Law

The magnetic field, dB at a point P due to an element of length ds that carries a current I is detailed in the following equation:

where:

r is the distance from the element to point P

vector r is the unit vector = 1

We find the total field at point P by integrating this expression over the entire current distribution 

Amperes Law:  

The law states the line integral     around any closed path is equal to permeability of free space times the enclosed current.

Gauss' Law for Magnetism states the total magnetic flux over a closed surface integral equals zero:

Magnitude of the magnetic field: where the field lines are concentric with the current carrying wire:

• B = [(uo)(I)]/[2pi(r)]

uo = permeability of free space

Where: 

 r = distance from a long straight wire carrying an electric current 

Magnitude of the field around a solenoid:

• B = [(N)(uo)(I)]/[2pi(r)]

uo = permeability of free space

Magnitude of the field around a toroid: 

• B = [(N)(uo)(I)]

uo = permeability of free space

Magnetic force per unit length between two parallel wires separated by a distance a, carrying current I1 and I2 has a magnitude of:

                                

= FB / legnth

Class Practice examples:

CP 11-06-13
BIOT-SAVART LAW 

1. Calculate the magnetic field outside am infinitely long, straight wire.

*set up in integral to find the Magnetic field (B) at point P

i) write the Biot Savart Law: 

ii) solve I(dl) x (r unit vector) = I(dl)(1)sin(a) = I(dl)sin(a)

iii) solve r^2    FIRST, SET AXIS & ORIGIN 

     r^2 = a^2 + x^2

iv) plug back everything back into the original equation

     dB = [(uoI(dl)sin(a)]/[4pi(a^2 + x^2)]

v) get dl in terms of x:

x = l 

vi) get r in terms of x

r = 1 unit vector 

vii) integrate[dB]dx from 0 -> infinity 

where uoI/4pi is a constant 

*note that the integral must be multiplied by 2 to encompass the entire infinite wire. 

2*(uoI/4pi) integral[dB = [(dx)sin(180)]/(a^2 + x^2)] from 0 -> infinity

2*(uoI/4pi) integral[dB = (dx)/(a^2 + x^2)] from 0 -> infinity

Conclusion: dl is always parallel to I, same direction!

AMPERES LAW

1. Find the magnetic field between 0 < r < R in a wire (imagine a cylindrical surface)

given: 

Current density (J) is uniform

R = radius 

infinite wire 

i) Create an Amperian loop 

• SURFACEint[B dot dl] = (uo)(I)

ii) pick an arbitrary direction for the current, I

iii) determine the symmetry of the problem to discuss and describe the magnetic field 

- If the magnetic field exists (B) it cannot change as you go around the loop. 

- At the origin, the physical situation at one point is the same at another point. 

- B is not a function of dl because due to the inherent symmetry of the universe. 

iv) solve the equation for the Amperian loop

SURFACEint[B dot dl] = (uo)(I)

[B] * SURFACEint[dlcos(theta)] = (uo)(I)

• Magnetic field (B) must be perpendicular to the current (I) and in the same plane as point P

           THEREFORE there can be no right or left component.  B is therefore tangent to to the                        current path. 

2. determine if the magnetic field is CW or CCW 

this can be accomplished using two different methods.

method 1: 

Use the RHR to determine the Current (I) path. 

Leave B as +/- 

Apply Amperes law

Solve for B (should be positive, magnitudes are always positive)

method 2:  apply amperes law 

i) select a direction for the magnetic field (CW or CCW)

• If B is in the direction of dl, the angle between +/- B and dl is 0
• If B is opposite of the direction of dl, the angle between +/- B and dl is 180
• If I is in the same direction as B, I is positive
• If I is opposite of the direction of B, I is negative.

Chapter 29: Magnetic Fields

The Magnetic Field 

UNIT: Tesla = 1(N/A)m

Typical magnets have a north and south pole:

• Field lines move NORTH --->SOUTH outside the magnet 
• Field lines move SOUTH ---> NORTH within the magnet

Strength of a magnetic field is proportional to the density of the magnetic field lines.

Fundamental difference between Electrical field lines and Magnetic field lines:

- Magnetic field lines move in closed loops. 

- Magnetic field lines continue through the magnet 

- Electric field lines form open loops

- Electric field lines start on positive charges and end of negative charges

Magnetic field is a function of vectors: F, v and q

Lorenz Force:
F on q = qV x B

where: v is the velocity of the charge relative to the observer 

• solving for the magnitude: C x D = CDsin(theta)
• solving for the direction: use the right hand rule 

* Force will always be perpendicular to Velocity

* Force will always be perpendicular to B 

   Force is a product of current, not charge

* B is defined as dF = Idl x B

RIGHT HAND RULE for the direction of current (I): 

• Particle Direction (I) = Direction of fingers
• Magnetic Field (B)   = Face palm / curl fingers
• Force of Current (F) = Direction of thumb

NOTE:
* Magnetic fields cannot ever do work on a charged particle!
* Force is always perpendicular to the current and motion 
* The electrical field can do work on a charged particle 

DEFINITION: magnetic dipole moment vector, u, of a loop carrying a current, I is = IA

Where the area vector, A is perpendicular to the plane of the loop and the magnitude of the area is equal to the area of the loop.

UNIT for the magnetic dipole moment vector, u: (A)(m)^2

Torque (t) in a current loop in a uniform magnetic field: 

• t = u x B 

To determine the total magnetic force on an ARBITRARILY shaped wire carrying a current (I), you must integrate the equation: 

• dFB = I ds x B

the potential energy of the system of a magnetic dipole in a magnetic field: 

• U = - uBcos(theta)

If a charged particle moves in a uniform magnetic field, where its initial velocity is perpendicular to the field, the particle moves in a circular path. The radius of the circular path is: 

• r = (mv)/(qB)

where:

m = mass of the particle 

q = charge of a particle v = angular speed of the charged particle = omega = w = qB/m

CYCLOTRON

• radius of a cyclotron: r = mv / qB

ac = centripetal acceleration

Cyclotron structure: moves particles to higher speeds every time it crosses the boundary between a "D":

*NOTE: magnetic fields cannot accelerate a particle
*NOTE: the electric field between the D's is what accelerates the particles; increasing KE each time it passes the D

frequency: the number of cycles per second between the D's, quantitatively:
UNIT: 1 Hz

• f = 1/T
• T = 2(pi)r/v 

*recall, the radius of a cyclotron: r = mv / qB

so, f = 1/T is equal to: qB/2(pi)m

the ELECTRIC FIELD is always perpendicular to the MAGNETIC FIELD in a cyclotron.

A cyclotron always uses an AC source - because it must be an alternating current to flip the field.

Torque on a loop of current:

Magnitude of torque: t = r x F 

Direction of torque: Right Hand Rule:

B = palm direction
I = fingers
mu = thumb

*When B is parallel to I(dl), net force is equal to zero

The magnetic moment vector: mu

mu = IA

Potential Energy in a magnetic field for a current loop:

t = (mu) x B

for an external agent to rotate a current loop; work must me don along a circular path:

UMPE = - (mu) dot (B) + constant

UMPE is the smallest when mu is parallel to B (0 degrees)

Positive work occurs when we try to move against the torque caused by external forces.
--> this causes an increase in the magnetic potential energy (UMPE)

HALL EFFECT

The hall effect answers the fundamental question about what is the nature of positive and negative mass. 

knowing electrons have mobility within atoms; the hall effect proves that current is the flow is positive electrons. 

The magnetic force that acts on a charge q moving with velocity vector v in a magnetic field, B:

• FB = I(dl) x B

Where dl is the path of the conductor carrying the current, in the direction of current

*FORCE is perpendicular to velocity  
*a is perpendicular to v

- when no other forces are present, the path is circular.

Can magnetic force do work on a particle?
No: only the electric field / force can do work on a particle 

Magnitude of the magnetic force: 

• FB = abs(q)(v)(B)sin(theta)

Where Theta is the acute (smaller) angle between velocity vector v and B 

CP#9 10-29-13

Find the radius of motion of a charged particle, +q with velocity vector, V and mass, m.

Step 1: set up a coordinate system (perpendicular to velocity)
Step 2:       Radius = SUM of all forces = (mass)(acceleration) 
                          R = -(q)(v)(B)sin(theta) = (mass)(acceleration)
                                                                                    *set acceleration = (-V^2/R)
                                                      R = -qvB = m(-V^2/R)                       
                                                                   R = mv/qB

Chapter 28: Direct Current Circuits

Chapter 28: introduces 'Direct Current Circuits' also known as DC circuits and "Resistor Capacitor Circuits, also known as RC circuits. 

DEFINITIONS:

Resistance is a function of temperature, it is the amount of voltage per unit of current across a resistor
UNIT: ohms

the emf of a battery is called the electromotive force 

emf of a battery is equal to the voltage difference across its terminals, when the current (I) = 0. This voltage situation is described as "open circuit voltage".

Equivalent resistance: when a set of resistors are connected and represented as one in a circuit diagram

Resistors in parallel:

• 1/Req = 1/R1 + 1/R2 + 1/R3 + ....

Resistors in series:

• Req = R1 + R2 +....

Circuits involving more than one loop are analyzed with Kirchoff's Rules: 

1. Junction Rule: at any junction the sum of the currents (I) must equal zero:

• Sum I = 0

2. Loop Rule: the sum of the potential differences across all elements around any circut loop must be zero:

• Sum (Vf-Vi) = 0

Steps to solve: 

1.  determine the number of loops 

loop 1: abefa

loop 2: bcdeb

       2.   "travel" each loop and write the Sum of Delta V = 0 for EACH CIRCUIT ELEMENT

Delta V = Vdownstream - Vupstream

for an ideal battery: I in the -  -->  + emf direction

• Delta V = + emf 

for an ideal battery: I in the +  -->  - emf direction

• Delta V = - emf 

for a resistor: 

I in the + ---> - direction 

• Delta VR = -IR

           3. set each loop equation equal to zero. solve for I. plug into the Junction Rule (1). Multiply the                  remaining equation by any common factor. Solve for a real value for I. Plug back in to find the                other value for I.

If a capacitor is CHARGED by a battery through a resistor (R), the charge on the capacitor and the current in the circuit vary in time:

• q(t) = Q(1-e^(-t/RC)) 

• I(t) = [emf / R]e^(-t/RC)

Q = C(emf) = maximum charge on the capacitor 

RC = time constant, T of the circuit 

****this is a differential equation. Why?

Answer: there is a derivative in the solution

If a charged capacitor is DISCHARGED through a resistor with resistance, R, the charge and current decrease exponentially in time: 

• q(t) = Qe^(-t/RC)

• I(t) = -Iie^(-t/RC)

Q = initial charge on the capacitor 

Ii = Q/RC = initial current in the circuit 

Chapter 27: Current and Resistance

Chapter 27: Current and Resistance introduces the concept of Current Density (J). We are provided a series of equations that compliment our understanding of "what is current density?"  "How do I utilize this concept to better understand the world?"

Current Density is a vector quantity that is defined as: J Units for J: Amps/m^2J points in the direction CURRENT IS FLOWING/MOVING.
J is a function of time and space.

Current Density (J) of an ohmic conductor is proportional to the electric field WHEN FLOW IS UNIFORM:

• J = (conductivity of the material)(Electric field)

NOTE: conductivity is not a function of E

Wait ... what is conductivity?

Google Definition says:
Conductivity is the degree to which a specified material conducts electricity, calculated as the ratio of the current density in the material to the electric field that causes the flow of current. It is the reciprocal of the resistivity.

therefore......

•  in the absence of an electric field, the average velocity of an electron equals zero
• current density is dependent on the electric field

This brings up the topic of OHMIC MATERIALS:

An ohmic material is a material in which the conductivity of the material is not a function of the electric field.

OHMS LAW

where V is the potential difference, aka: voltage difference, delta V, voltage change

*NOTE: when voltage increases, current increases!

Now, back to the topic of current density....

WHEN FLOW IS NOT UNIFORM, what is the current density?

NOTE: J is perpendicular to the surface
NOTE: J and dA are always paralell
NOTE: I = int[J(A)dA]

Additional useful equations from this topic:

The average current in a conductor is related to the motion of the charge carriers:

• Iavg = nqvA

n= density of charge carriers
q = charge on each carrier
v = drift speed
A = xsection areaof the conductor

The resistance over length "l" for a uniform block with a xsection area "A":

• R = (rho)[(l/A)]

rho = resistivity of the material (given in a table, or google it!)

resistance is equal to the resistivity constant, rho: p multiplied by the length of the object, all divided by the area of the object:

Resistivity of a conductor varies linearly with temperature according to this equation: 

• rho = rhoo[(1+alpha(T-To)]

Questions to think about:

Is RESISTANCE the same as RESISTIVITY? 

NO: resistivity is an intrinsic material property that is found on a table (or on google....) 

How is conductivity related to RESISTIVITY?

Conductivity is inversely proportional to resistivity. when conductivity goes down, resistivity goes up!

METALS: have high conductivity, low resistivity

INSULATORS: have low conductivity, high resistivity 

Class Practice from lecture*: 10-7-13

1. Given the VAVG, q, A, n find the current (I).

total # charges = n(volume) = n(area)
               
             total # electrons that cross = n(A)(VAVG)(T2-T1)

Q2-Q1 = total charge = (#)(q)
Q2-Q1 = total charge = [n(A)(VAVG)(T2-T1)][q]
                 
I = Q2-Q1 / T2-T1

I = [n(A)(VAVG)(T2-T1)](q)] / (T2-T1)
I = nA(VAVG)q

2. Calculate the total amount of blood flow **friction is involved!!**

*note: when R = 0, flow is at a maximum
*note: when r = R flow is at a minimum

 - find the current: 

I = integral[J(A)(d(a)(cos(0))] 

I = integral[J(R)2pi(r)dr] from 0 -> R

I = integral[Ji - (Ji/R)^r(2pi(r)dr)] from 0 -> R

I = integral[Ji 2pi(1-(1/R)^r)dr] from 0 -> R

I = 2piJi [(r^2/2)-(r^3/3R)]^r from 0 -> R

3. In a wire, J is not dependent upon dA. Give the equation for I in terms in J and A. **NO Friction!**

I = (Q2-Q1)/(T2-T1) 
I = integral[J dot dA] 
I = (J)integral[dA]
I = JA

for wires:
Current = I = JA
                J = I/A
4. Given that I = (n)(q)VAVG(A), find an expression for J in a wire:

J = (n)(q)(VAVG)
where n = charge density 


*(P. Francis, De Anza College, Physics 4B lecture on chapter 27)

ELECTRICAL POWER: "the rate of doing work"

P = power of the battery
Unit for Power: Joules/second = Watt

Power: is the rate at which energy us being converted from chemical to electric potential energy & thermal energy (heat loss).

• PBATT = V(dQ/dt) = (V)(I)

                                                               memorization tip: P=IV  can be pronounced: "peev"

* for an OHMIC material:

• PBATT = (I)^2(R)

where
 I(t) is a function of time

If a potential difference is maintained across a circus element, the power (aka rate of energy supplied to the element) is:

• Power = I(Vf-Vi)

Power delivered to a resistor: 

• P = (I)^2R = (Vf-Vi)^2 / R

Why can we describe the power delivered to a resister with this equation?
Answer: because the potential difference across a resister is (Vf-Vi) = IR

Work done by power: 
from t=o to t=end



Example from lecture (P. Francis, De Anza College, Physics 4B)

Calculate the resistance of the right 1/3 of the material shaped as a cone:

step 1: find A(x)

A(x) = pi(r)^2
where r = (slope)x+b
where b =0
r = (slope)x
r = (R/H)x

step 2: integrate

R = int[p(dx)/[pi(R^2/H^2)x^2]] from 2/3H to 1H

Additional equations introduced in this chapter: 

When an electric field is applied the average velocity of electrons is equal to the Drift Velocity vd

• vd = [(q)(E)/me]T

T = average time interval between electron-atom collisions
me = mass of the electron

According to this model, the resistivity of metal is:

• rho = [me / (n(q)^2T)]